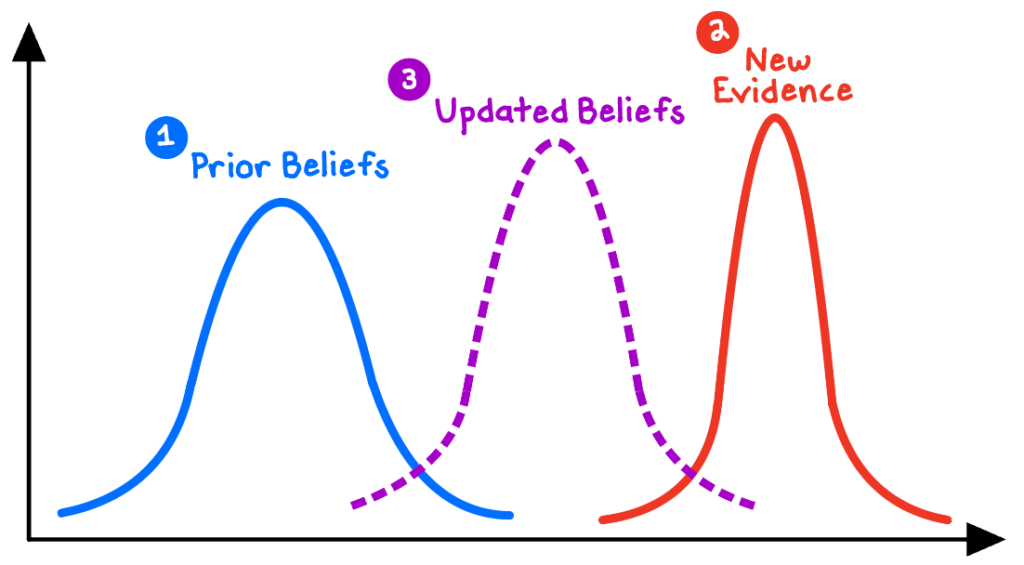
Bayesian reasoning is a structured approach to incorporating probabilistic thinking into our decision making. It requires two key steps:
- Obtain informed preexisting beliefs (“priors”) about the likelihood of some phenomena, such as a suspect’s DNA matching the crime scene evidence, a candidate winning an election, or an X-ray revealing a tumor.
- Update our probability estimates mathematically when we encounter new, relevant information, such as finding DNA from a new suspect, a new poll revealing shifting voter behavior, or a new X-ray showing unexpected results.
The Bayesian approach allows us to use probabilities to represent our personal ignorance and uncertainty. As we gather more good information, we can reduce uncertainty and make better predictions.
Unfortunately, when we receive new information, we tend to either (a) dismiss it because it conflicts with our prior beliefs (confirmation bias) or (b) overweight it because we can recall it more easily (the availability heuristic). Bayesian reasoning demands a balancing act to avoid these extremes: we must continuously revise our beliefs as we receive fresh data, but our pre-existing knowledge—and even our judgment—is central to changing our minds correctly. The data doesn’t speak for itself. 1
The Bayesian approach rests on an elegant but computationally intensive theorem for combining probabilities. Fortunately, we don’t always need to be able to crunch probability calculations, because Bayesian reasoning is extremely useful as a rule of thumb: good predictions tend to come from appropriately combining prior knowledge with new information.
However, as we will see, Bayes is simultaneously super nifty and incredibly limited—as all rules of thumb are.
Why your Instagram ads are so creepy
We experience Bayesian models constantly in today’s digital world. Ever wondered why your Instagram ads seem scarily accurate? The predictive models used by social media apps are powerful Bayesian machines.
As you scroll to a potential ad slot, Instagram’s ad engine makes a baseline prediction about which ad you’re most likely to engage with, based on its “priors” of your demographic data, browsing history, past engagement with similar ads, etc. Depending on how/whether you engage with the ad, the ad targeting algorithm updates its future predictions about which ads you’re likely to interact with.2 This iterative process is the reason why your ads seem creepy: they become remarkably accurate over time through constant Bayesian fine-tuning.
Prioritize priors
For Bayesians, few things are more important than having good priors, or “base rates,” to use a a starting point—such as the demographic or historical-usage data on your Instagram account.
In practice, we tend to underweight or neglect base rates altogether when we receive case-specific information about an issue. For example, would you assume that a random reader of The New York Times is more likely to have a PhD, or to have no college degree? Though Times readers are indeed likely to be more educated, the counterintuitive truth is that far fewer readers have a PhD, because the base rate is much lower!3 There are over 20x more Americans with no college degree than those with a doctorate.
The prescription to this error (called “base-rate neglect”) requires anchoring our judgments on credible base rates, and thinking critically about how much weight to assign to new information. Without any useful new information (or with worthless information), Bayes provides us clear guidance: hold to the base rates.
“Pizza-gate”
Many bad ideas come from neglecting base rates.
Consider conspiracy theories, which, despite their flimsy core claims, propagate by including a sort of Bayesian “protective coating” which discourages believers from updating their beliefs when new information inevitably contradicts the theory.
For example, proponents of the “Pizza-gate” conspiracy falsely claimed in 2016 that presidential candidate Hillary Clinton was running a child sex-trafficking ring out of a pizzeria in Washington, DC. A good Bayesian would assign a very low baseline probability to this theory, based on the prior belief that such operations are exceedingly rare—especially for a lifelong public servant in such an implausible location.
When the evidence inevitably contradicts or fails to support such a ludicrous theory, we should give even less credence to it. That is why Pizza-gate proponents, like many conspiracy theorists, introduced a second, equally baseless theory: that a vast political-media conspiracy exists to cover up the truth! The probability of this second theory is also really low, but it doesn’t matter.4 With this “protective layer” of a political-media cover-up, conspiracy theorists can quickly dismiss all the information that doesn’t support the theory that Hillary Clinton must be a pedophilic mastermind.
Bayesian reasoning is only as good as the priors it starts with, and the willingness of its users to objectively integrate new, valid information.
The boundaries of Bayes
The mathematics of Bayes’ theorem itself is uncontroversial. But Bayesian reasoning becomes problematic when we treat it as anything more than a “rule of thumb” that’s useful when we have a comprehensive understanding of the problem and very good data.
Estimating prior probabilities involves substantial guesswork, which opens the door for subjectivity and error to creep in. We could ignore alternative explanations for the evidence, which is likely to lead us to simply confirm what we already believe. Or, we could assign probabilities to things that may not even exist, such as the Greek gods or the multiverse.5
The biggest problem: Bayes cannot possibly create new explanations. All it can do is assign probabilities to our existing ideas, given our current (incomplete) knowledge. It cannot generate novel guesses. But sometimes, the best explanation is one that has not yet been considered. Indeed, creating new theories is the purpose of science. Scientific progress occurs as new and better explanations supersede their predecessors. All theories are fallible. We may have overwhelming evidence for a false theory, and no evidence for a superior one.
A great example is Albert Einstein’s theory of general relativity (1915), which eclipsed Isaac Newton’s theory of gravity that had dominated our thinking for two centuries. Before Einstein, every experiment on gravity seemed to confirm Newtonian physics, giving Bayesians more and more confidence in his theory. That is, until Einstein showed that Newton’s theory, while extremely useful as a rule of thumb for many human applications, was completely insufficient as a universal theory of gravity. Ironically, the day before Newton’s theory was shown to be false was the day when we were most confident in it.6
The “probability” of general relativity is irrelevant. We understand that it is only conditionally true because it is superior to all other current rivals. We expect that relativity, as with all scientific theories, will eventually be replaced.7
***
Bayesian reasoning teaches us to (1) anchor our judgments on well-informed priors, and (2) incorporate new information intentionally, properly weighting the new evidence and our background knowledge. But we must temper our use of Bayesian reasoning in making probability estimates with the awareness that the best explanation could be one that we haven’t even considered, or one for which good evidence may not yet exist!
Notes
- Spiegelhalter, D. (2021). The Art of Statistics. Basic Books. 306-313.
- Horwitz, J., & Rodriguez, S. (2023, January 27). Meta Embraces AI as Facebook, Instagram Help Drive a Rebound. The Wall Street Journal.
- Kahneman, D. (2011). Thinking, Fast and Slow. Farrar, Straus and Giroux. 151-153.
- Ellenberg, J. (2015). How Not to Be Wrong. The Penguin Press. 183-184.
- Horgan, J. (2016, January 4). Bayes’s Theorem: What’s the Big Deal? Scientific American.
- Ravikant, N., & Hall, B. (2021, December 22). The Beginning of Infinity, Part 2. Naval Podcast.
- Hall, B. (2016). Bayesian “Epistemology” [Blog post].