The expected value of a process subject to randomness is the average of its outcomes, each weighted by its probability. We might use expected value to evaluate a variety of phenomena, such as the flip of a coin, the price of a stock, the payoff of a lottery ticket, the value of a bet in poker, the cost of a parking ticket, the decision of a business to launch a new product, or the utility of reading a book. The underlying principle of expected value is that the value of a future gain (or loss) should be directly proportional to the chances of getting it.
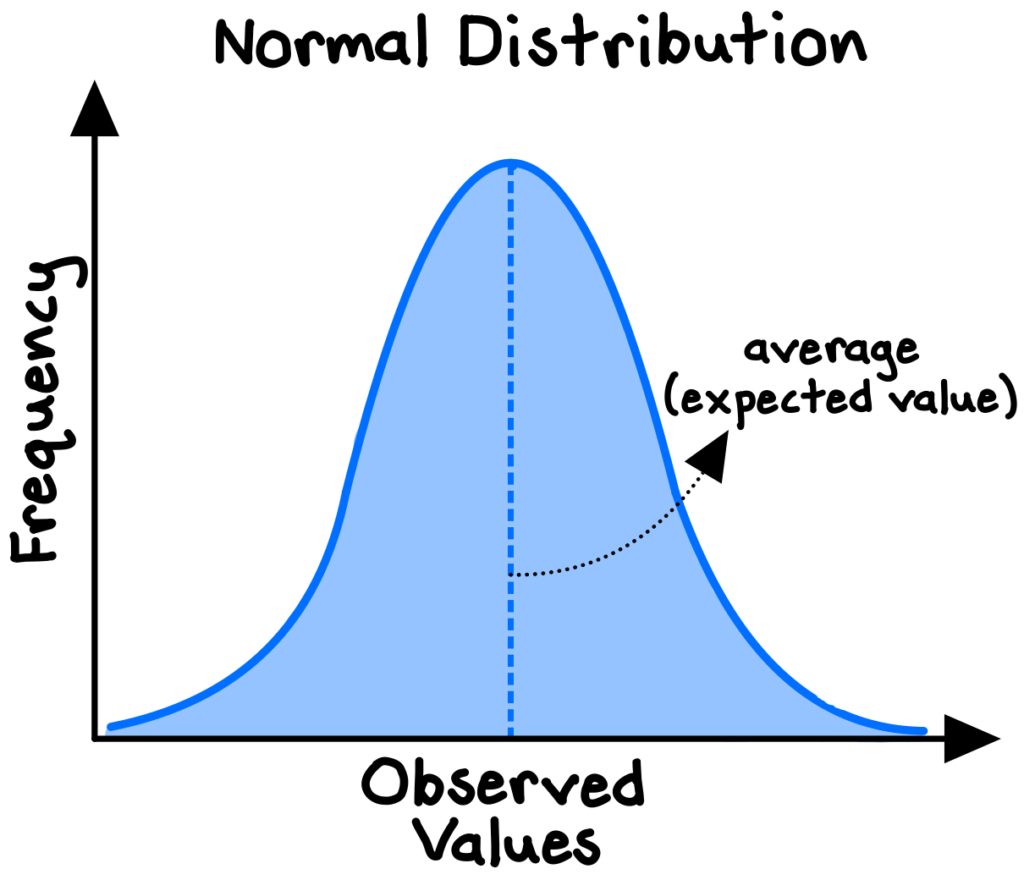
The concept originated from Pascal and Fermat’s solution in 1654 to the centuries-old “problem of points,” which sought to divide the stakes in a fair way between two players who have ended their game before it’s properly finished. Instead of focusing on what had already happened in the game, they focused on the relevant probabilities if the game were to continue. Their findings laid the foundations for modern probability theory, which has broad applications today, including in statistics (the mean of a normal distribution is the expected value), decision theory (utility-maximization and decision trees), machine learning algorithms, finance and valuation (net present value), physics (the center of mass concept), risk assessment, and quantum mechanics.
Expected value is one of the simplest tools we can use to improve our decision making: multiply the probability of gain times the size of potential gain, then subtract the probability of loss times the size of potential loss.
Simply put, we should bias towards making decisions with positive expected values, while avoiding decisions with negative ones. The idea is that, over the long run, we will be better off if we repeatedly select the alternatives with the highest expected values.
Useful but used wrongly
Lotteries are a classic example. We might genuinely enjoy playing the lottery. But we can’t ignore that lottery tickets are typically really bad bets, even when the jackpot is huge. Because the state takes a cut of the total pot and only pays out the remainder to winners, the expected value for all players must be negative.1
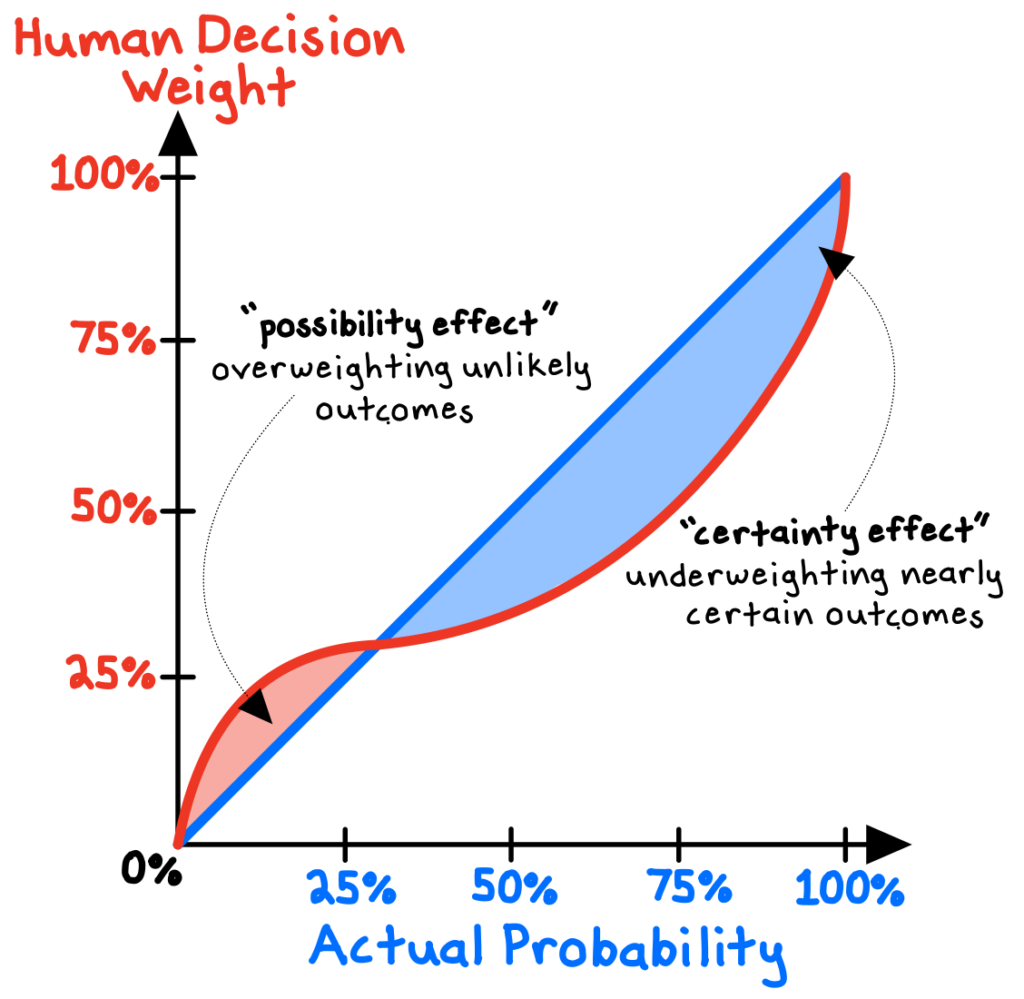
The expected value rule of thumb may seem straightforward, but a body of fascinating psychological research—particularly the work of Daniel Kahneman and Amos Tversky on “prospect theory”—shows that the decision weights that people assign to outcomes systematically differ from the actual probabilities of those outcomes.
For one, we tend to overweight extreme (low-probability) outcomes (the “possibility effect”). As a result, we overvalue small possibilities, increasing the attractiveness of lotteries and insurance policies. Second, we give too little weight to outcomes that are almost certain (the “certainty effect”). For example, we weigh the improvement from a 95% to 100% chance much more highly than the improvement from, say, 50% to 55%.2
Process over outcome
The expected value model reminds us to be more critical of the process (how we value the possibilities) than the outcome (what we actually get). When randomness and uncertainty are involved—as they almost always are in complex systems—even our best predictions will be wrong sometimes. We can’t perfectly anticipate or control such outcomes, but we can be rigorous with our preparation and analysis.
Remember, too, that expected value doesn’t represent what we literally expect to happen, but rather what we might expect to happen on average if the same decision were to be repeated many times (a better name might have been “average value”). Often we don’t and can’t know the exact expected value, but we can say with some confidence whether it’s positive or negative.4
Seeking the “long tail”
In some circumstances, applying expected values may be an entirely misguided approach. We must consider carefully the distribution of the underlying data. For a standard, normally distributed system (e.g., human height, SAT scores), the expected value is also the central tendency of the data, and is therefore a reasonable guess for any individual observation.
However, for power-law distributed systems (e.g., the frequency of words in the English language, the populations of cities), there are a small number of inputs that account for a highly disproportionate share of the output, skewing the distribution of the data. Because power laws are asymmetrical distributions, the expected value is not the central tendency of the data; a few extreme observations wildly skew the results.
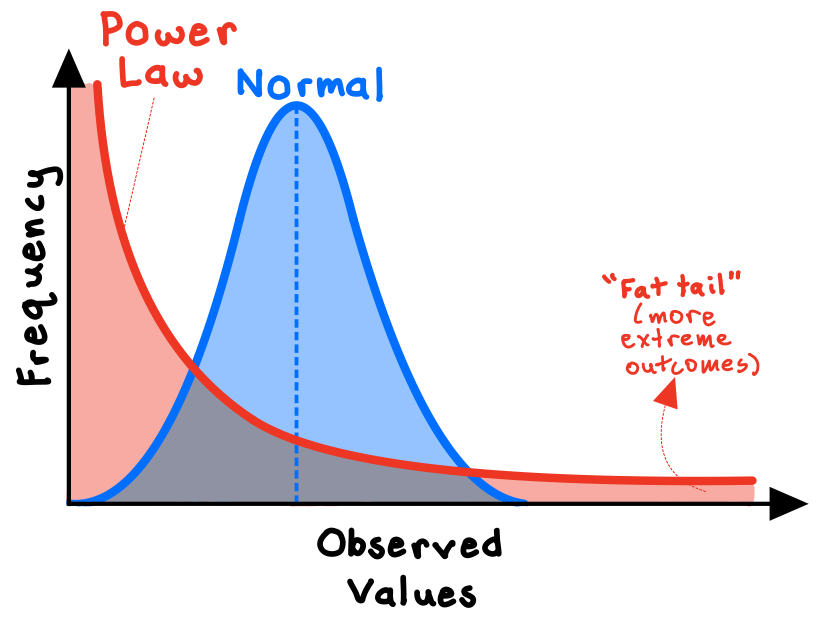
Consider the early-stage venture capital industry, in which investors put money into highly risky startup ventures. Financial returns on venture capital investments are power-law distributed. Most of these startups will fail, but the ones that do succeed can really succeed and generate massive financial returns (think Google or Tesla). Thus, for venture capitalists, the game is not to seek the average return or “expected value,” but rather to search for the “long tail”—the extreme outliers that generate outsized results.
Expected value is a lot less relevant when you don’t care as much about the probability of success than you do about the magnitude of success, if achieved. If one or two “grand slams” can generate massive returns for the fund, then VCs don’t care if 90% of their other investments fail.
Union Square Ventures, for example, invested in Coinbase in 2013 at a share price of about $0.20, and realized a massive return when Coinbase opened its initial public offering at $381 in 2021—a valuation of around $100bn and an increase of over 4,000x from the round that Union Square led eight years earlier.5
***
Expected value helps us evaluate alternatives even when we face substantial uncertainty our risk. Estimate the potential “payoffs” and weight them by their respective probabilities. In general, err towards making bets with positive expected values, while declining bets with negative ones.
While extremely useful as a rule of thumb, applying expected value can involve substantial subjectivity—and is therefore at risk of bias and error. Use ranges instead of single values to avoid false-precision. And remember that expected value may be entirely inappropriate when dealing with power-law distributed systems, where its not the “middle” outcome that dominates, but the “extreme” ones.
Notes
- Ellenberg, J. (2015). How Not to Be Wrong. The Penguin Press. 201-206.
- Kahneman, D. (2011). Thinking, Fast and Slow. Farrar, Straus and Giroux. 316-319.
- Kahneman, D. (2011). 315.
- Ellenberg, J. (2015). 354-357.
- Levy, A. (2021, April 14). Here’s who just got rich from the Coinbase debut. CNBC.