Exponential growth occurs whenever a stock of some material or quantity increases or replicates itself in constant proportion to how much there already is. This is a multiplicative effect, in which each step is more extreme than the preceding one. As an example, consider a stock of 1,000 hogs that, given its rates of fertility and mortality, grows exponentially at 10% per year. In the first year, there’s an increase of 100 hogs, then 110 in the second year, then 121 in the third year, and so on—illustrating the snowballing effect.
This type of growth contrasts sharply with linear growth, in which the stock changes by a constant quantity each period (an additive effect). If the hog population grew by a fixed 100 hogs annually, the implied percentage growth rate would diminish over time—from 10% in the first year to 9.1% in the second, and so on.
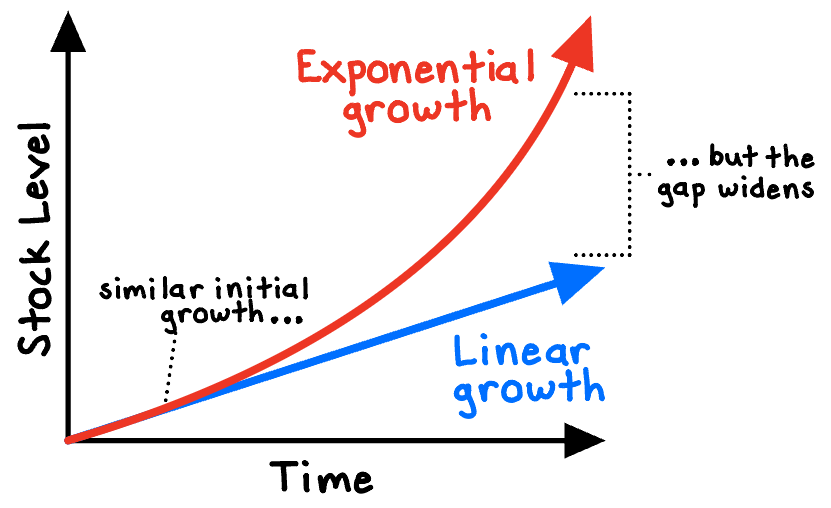
Exponential patterns are ubiquitous, from biological phenomena such as population growth and disease spread, to economic phenomena such as GDP growth and compound interest, to technological trends such as network effects in communications networks and improvements in the processing power of computers (“Moore’s law”).
Despite the prevalence of exponential progressions, our human intuition often fails to appreciate their speed and chaotic potential. Instead, we gravitate towards linear thinking because it serves us well in most practical circumstances. We can commit fewer errors and better explain and predict the world once we understand the power of exponential growth, and its equally powerful ability to unravel.
Feedback loops: Accelerators and regulators
The underlying driver of exponential growth lies in reinforcing (positive) feedback loops, which exist whenever a system (such as a virus or a savings account) can self-multiply or grow as a constant fraction of itself. These amplifying forces generate exponential growth, producing either virtuous or vicious cycles.
In contrast, balancing (negative) feedback loops are stabilizing, goal-seeking functions that aim to maintain a system in a given range of acceptable parameters—in a “dynamic equilibrium.” Consider how a thermostat regulates the temperature of a home, or how our bodies induce perspiration and shivering to stabilize our body temperatures.1
In physical systems that are growing exponentially, there must be at least one positive feedback loop propelling the growth, but there must also be at least one negative feedback loop constraining the growth, because no physical system can grow forever in a finite environment.2
The inevitable decay
Consider a virus such as COVID-19, which initially spreads exponentially through the population as each infected person infects multiple others. It might seem like an uncontrollable plague.
But again, nothing grows forever. The flip side of exponential growth is exponential decay, when a quantity decreases at a rate proportional to its current value. If we withdraw 10% of the funds in our savings account every period, the accounts’ value will decay exponentially in a downward reinforcing feedback loop.
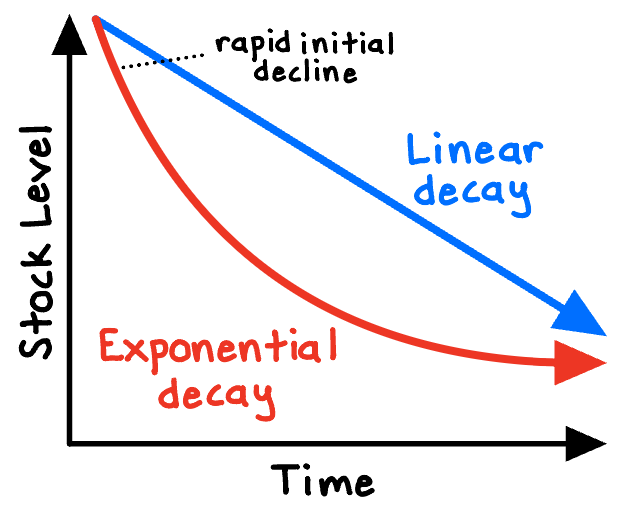
Let’s return to our example of a virus such as COVID-19 or smallpox. Over time, balancing feedback loops will kick in to combat the spread. In the worst case, the virus could simply start running out of people to infect because so many get sick. But eventually, even highly contagious viruses run out of steam. Our bodies will start to develop antibodies to increase immunity. Widespread vaccinations can achieve the same effect. Governments, organizations, and individuals may adapt their behavior to mitigate the risk and impact of the virus (wearing masks, providing aid, social distancing, etc.).
Once the average number of people that one infected person infects (the so-called “R-knot”) falls below the critical level of 1, the exponential growth turns to exponential decay, and the virus begins to die out. This is known as “herd immunity,” when there are not enough new hosts to whom the virus can continue to spread. The key insight for epidemic control is that “perfection” is not necessary; we don’t have to stop all transmission, just enough transmission to achieve herd immunity.3
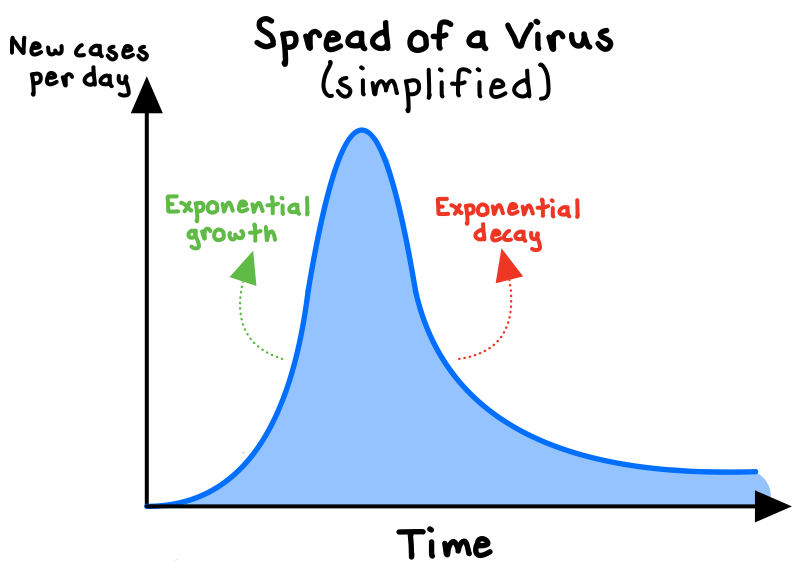
We can find exponential decay progressions in a variety of real-world applications, including the biological half-life of chemicals or drugs, the rate of radioactive decay by which nuclear material disintegrates, the decrease in atmospheric pressure at increasing heights above sea level, and the effectiveness of advertising messages over time.
Many phenomena exhibit both exponential growth and exponential decay, at different phases in their progressions.
The ascent and fall of Clubhouse
In 2020-21, Clubhouse, a live audio chatroom app, experienced a meteoric rise, growing to tens of millions of downloads within months. Its exponential growth was fueled by network effects, a type of positive feedback loop in which each new user makes the network more valuable to all other users. Notable celebrities and influencers joined in, creating more buzz and attracting more users around the app’s aura of novelty and exclusivity.
However, after its initial surge, Clubhouse ran into numerous challenges. Its pandemic-driven novelty diminished. Many celebrities and business leaders moved on. It was also difficult for users to engage consistently with live audio due to their busy schedules and fickle attention spans; podcasts and audiobooks remained much more convenient.
Perhaps above all, existing social media giants such as Facebook and Twitter appreciated the potential of the live audio format and moved rather quickly to copy Clubhouse’s functionality. It turned out that live audio was more promising as a feature of the existing platforms—which already had hundreds of millions of users—rather than as a standalone service that would need to bootstrap network effects from the ground up. Users could simply engage with live audio content within their existing social media routines.
The app’s new downloads declined by over 90% between February and April 2021.4 As signups slowed and users either churned or migrated to a competing service, the app became less valuable to both new and existing users—exacerbating its decline. Clubhouse experienced first-hand the capricious potential for exponential growth to unravel.
***
Whether with a virus, a population, or a company, we must remember that infinite exponential growth is mostly a theoretical construct. In the physical and practical world, there are always limits. Exponential growth may only occur across a particular scale of observation—such as during the initial contagion of a virus (when few people have been exposed), or during the early period of a new product’s life (when novelty is high and competition is low). Balancing feedback loops ultimately tame exponential progressions.
We must not underestimate the speed with which exponential forces can generate explosive growth—or equally rapid decline!
Notes
- Meadows, D. (2008). Thinking in Systems: A Primer. Chelsea Green Publishing. 27-30.
- Meadows, D. (2008). 59.
- Ellenberg, J. (2021). Shape. Penguin Press. 218-222.
- Fatemi, F. (February 10, 2022). The Rise And Fall Of Social Audio Will Continue To Impact The Entertainment Industry For The Next Generation. Forbes.