A fundamental objective of exploring data is to unearth the factors that explain something. For example, does a new drug explain an improvement in a patient’s condition? Does the DNA evidence match the suspect’s? Does the new product feature improve user engagement?
The reigning theory of knowledge, Karl Popper’s critical rationalism, tells us how we cultivate good explanations. Simply put, we start by guessing. We then subject our best guesses to critical tests, aiming to disprove them. Progress emerges from the trial-and-error process of eliminating ideas that fail such tests and preserving those that survive.1
These guesses, or hypotheses, are not “ultimate truths.” They are tentative, temporary assumptions—like a list of suspects for an unsolved crime.
But how do we objectively evaluate these guesses? Fortunately, statistics provides a solution.
Hypothesis testing is a formal statistical procedure for evaluating the support for our theories. It is hard to understate the huge role this methodology plays in science. It teaches us how to interpret important experimental results and how to avoid deceptive traps, helping us systematically eliminate wrongness.
Feeling insignificant?
Typically with hypothesis testing, we are referring to the null hypothesis significance test, which has been something of a statistical gold standard in science since the early 20th century.
Under this test, a form of “proof by contradiction,” it is not enough that the data be consistent with your theory. The data must be inconsistent with the inverse of your theory—the maligned null hypothesis.
The null is a relentlessly negative theory, which always postulates that there is no effect, relationship, or change (the drug does nothing, the DNA doesn’t match, etc.). It is analogous to the “presumption of innocence” in a criminal trial: a jury ruling of “not guilty” does not prove that the defendant is innocent, just that s/he couldn’t be definitively proven guilty.2
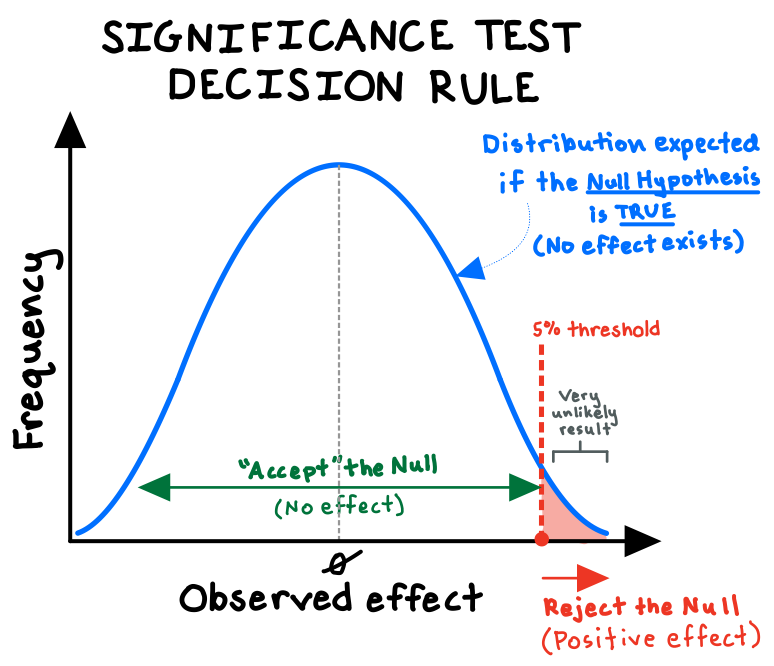
Say we wanted to run a clinical trial to test whether our new drug has a positive effect. We define our null hypothesis as the claim that the drug does nothing, and we plot the expected distribution of those results (the blue bell-shaped curve below). Then, we run an experiment, with a sufficiently large and randomly selected group of subjects, that attempts to refute the null at a certain “significance level”—commonly 5% (see red shaded area below).
The significance level (or “p-value”) represents the probability of observing a result as extreme as we did if the drug actually had no effect—that is, if random variation alone could adequately explain our results. For us to reject the null and claim that our trial provides “statistically significant” support for our drug, we need the observed improvement in our patients’ conditions to be large enough that our p-value very low (below 5%)!
A or B?
We can apply hypothesis testing methods to evaluate experimental results across disciplines, such as whether a government program demonstrated its promised benefits, or whether crime-scene DNA evidence matches the suspect’s.
Essentially all internet-based companies (Twitter, Uber, etc.) use these same principles to conduct “A/B tests” to evaluate new features, designs, or algorithms. Just as with our clinical trial example, the company exposes a random sample of users to the new feature, then compares certain metrics (e.g., click-rate, time spent, purchase amount) to those of a control group that doesn’t receive the feature. Whichever iteration performs best wins. For any app on your phone, its creator likely conducted dozens of A/B tests to determine the combination of features and designs that you see, down to the tempting color of the “Purchase” button!
Stop, in the name of good statistics
Failing to understand hypothesis testing guarantees that we will be wrong more often. Too many people blindly accept faulty or pseudo-scientific experimental results or catchy headlines. They sometimes choose to ignore the science altogether, preferring to craft simple, tidy narratives about cause and effect (often merely confirming their preexisting beliefs).
Even if we do take the time to consider the science, hypothesis testing is far from perfect. Three main points of caution:
- First, achieving statistical significance is not synonymous with finding the “truth.” All it can tell us is whether the results of a given experiment—with all its potential for random error, unconscious bias, or outright manipulation—are consistent with the null hypothesis, at a certain significance level.
- Second, significance ≠ importance. To “reject” the null hypothesis is simply to assert that the effect under study is not zero, but the effect could still be very small or not important. For example, our new drug could triple the likelihood of an extreme side effect from, say, 1-in-3 million to 1-in-1 million, but that side effect remains so rare as to be essentially irrelevant.3
- Third, a significance test, by definition, has only a certain degree of precision which is never 100%. And improbable things happen all the time. For example, a significance level of 5% literally implies a 1-in-20 chance of incorrectly accepting experimental results as true. This enables the nasty “multiple testing” problem, which occurs when researchers perform many significance tests but only report the most significant results. For example, if we do 10 trials of a useless drug with a 5% significance level, the chance of getting at least one statistically significant result gets as high as 40%! You can see the incentive for ambitious researchers—who seek significant results they can publish in prestigious journals—to tinker obsessively to unearth a new “discovery.”4
***
Used properly, hypothesis testing is one of the best data-driven methods we have to evaluate hypotheses and quantify our uncertainty. It provides a statistical framework for the “critical tests” that are indispensable to Popper’s trial-and-error process of knowledge creation.
If you have a theory, start by exploring what experiments have been done about it. Review multiple studies if possible to see if the results have been replicated. And if there aren’t any prior research studies, be careful before making strong, unsubstantiated claims. Even better, see if you or your company can perform your own experiment!