“Here, on the edge of what we know, in contact with the ocean of the unknown, shines the mystery and beauty of the world. And it’s breathtaking.”
Carlo Rovelli, Seven Brief Lessons on Physics (2016, pg. 81)
Despite our human programming to detect patterns and seek causes or explanations for everything we observe, many events in the world are simply chaotic and unpredictable. Failures to properly account for randomness lead us astray constantly, especially when we are operating in complex systems such as an economy, company, country, or ecosystem.
Our human tendency to craft neat, linear narratives about cause-and-effect can fool us into identifying causal connections between events where none actually exists (such as a relationship between astrological signs and personality traits). It also leads us to naively extrapolate that what has happened in the past will continue into the future. In our interpersonal interactions, we tend to over-attribute people’s behavior to inherent characteristics, versus circumstantial factors or chance. Overall, these fallacies give us false confidence that things are more predictable and explainable than they really are.1
“We are far too willing to reject the belief that much of what we see in life is random.”
Daniel Kahneman, Thinking, Fast and Slow (2011, pg. 117)
But we can, sometimes, harness the chaos. Randomness can work to our advantage, whether in business, computer science, statistics, or—indeed—in the evolution of all life forms. But first…
Why so random?
Is the world inherently random and unpredictable? Physics offers some intriguing insights.
In classical physics, which describes everyday events such as rolling billiard balls and orbiting planets, “random” behavior can emerge from phenomena that are completely orderly and predictable—at least in theory. The problem in practice is twofold. First, perfect prediction requires a flawless understanding of the laws of nature, which we may never achieve. Second, it also requires an impossibly precise knowledge of the system’s initial conditions.2 Whether we’re measuring the motion of a billiards ball or a planet, no instrument can provide infinite precision. Approximation is our best hope. With time, even small errors in these specifications can lead to huge errors in the prediction (the “butterfly effect”). For this reason, many events—the weather, stock market, highway traffic—may appear “random” simply because we can’t gather and process data quickly enough to predict them.
However, in quantum physics, the other pillar of modern physics, which studies microscopic phenomena, unpredictability may go deeper. The observed behaviors of the universe’s most basic particles are notoriously random. Even if we had perfect information of their initial positions and velocities, we can only make probabilistic predictions of where they will go.3 The universe, it seems, will always be full of surprises!
Taming randomness with numbers
But the value of randomness is not limited to the cautionary tale that “we can’t perfectly predict things.” Randomness is a versatile, multidisciplinary mental asset—particularly in the field of statistics.
While individual random events (particle movements, coin flips) are unpredictable, if we know the “distribution” of the underlying data, the probability of different outcomes over a large enough sample size becomes predictable. This principle lies at the heart of statistics, producing tools such as the well-known normal distribution, which can help us quantify uncertainty and make useful inferences and predictions even for random events. In quantum physics, we can predict the probability distribution of a particle’s movements with remarkable accuracy, but we can never be certain of its exact behavior on any particular observation.
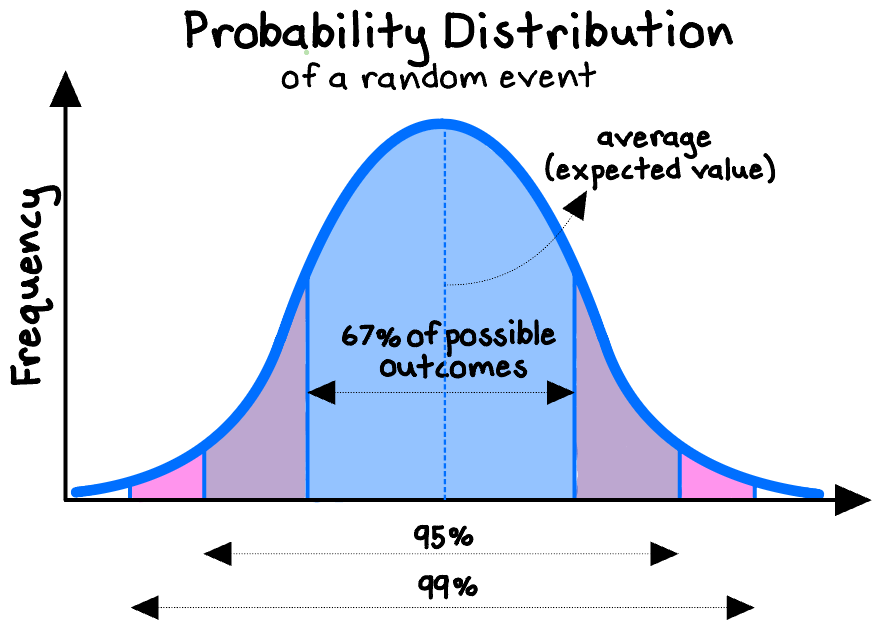
When faced with a problem too complex to be understood directly, one of the best tools we have to begin to untangle it is to collect a random sample and closely study the results. In scientific experiments aiming to assess causality (for example, whether a new dieting method causes weight loss), randomness is a critical ingredient. A valid experiment requires randomization both in (1) selecting a sample from the target population to study, and (2) assigning the subjects to “treatment” versus “control” groups. True randomization ensures that on average a sample resembles the population, enabling us to make valid inferences about that population.4
Without truly randomized sampling in our experiments, we are likely to generate biased and misleading results. If, for instance, all the subjects in our clinical trial were American adult men (as was the case for decades), our sample may not be representative of the patients we intend to treat.
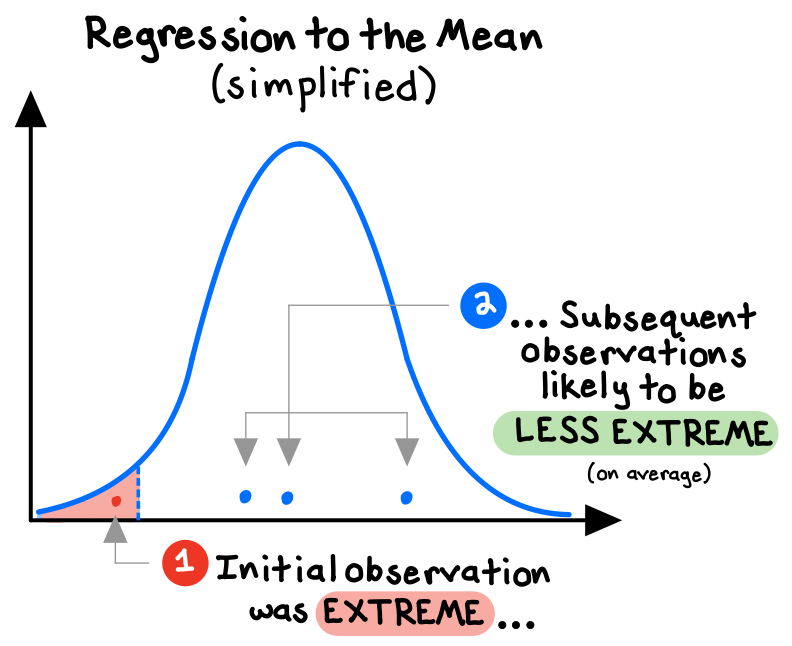
Randomness is also the explanation behind regression to the mean: when there is some amount of randomness involved in an event, we should expect extreme outcomes to be followed by more moderate outcomes, because some extreme results are simply blind luck. And luck is transitory.
For example, because our body weight fluctuates daily, the heaviest participants in a new diet study are certainly more likely to have a consistent weight problem (an inherent trait), but they are also more likely to have been at the high-end of their weight range on the day we first weigh them (a random fluctuation). Therefore, the heaviest patients at the beginning of the study should, on average, be expected to lose some weight over time, regardless of the treatment being studied.5 To get a useful signal, we need to compare the results of the “treatment group” to those of a “control group” that did not try the diet. Otherwise, any “discovery” we make could simply be the (predictable) result of randomness!
Solving problems with chaos
Whenever we encounter a problem we’re not sure how to solve, injecting a bit of randomness into the process can often unearth unique and unexpected solutions. If the solution seems elusive, we should ask ourselves whether we can simply try something, learn from whatever happens, and adjust from there.
Nature itself has mastered the art of trial-and-error. In evolutionary biology, random variation in the copying of genes enables the incredible adaptations and life forms we observe in nature. First, the imperfect process of copying genes from parent to offspring creates random mutations, with no regard to what problems those variants might solve. Over time, nature will “select” for the genes most successful at causing themselves to be replicated in the future, such as those that cause better brain function in humans, prettier feathers in peacocks, or longer necks in giraffes.6
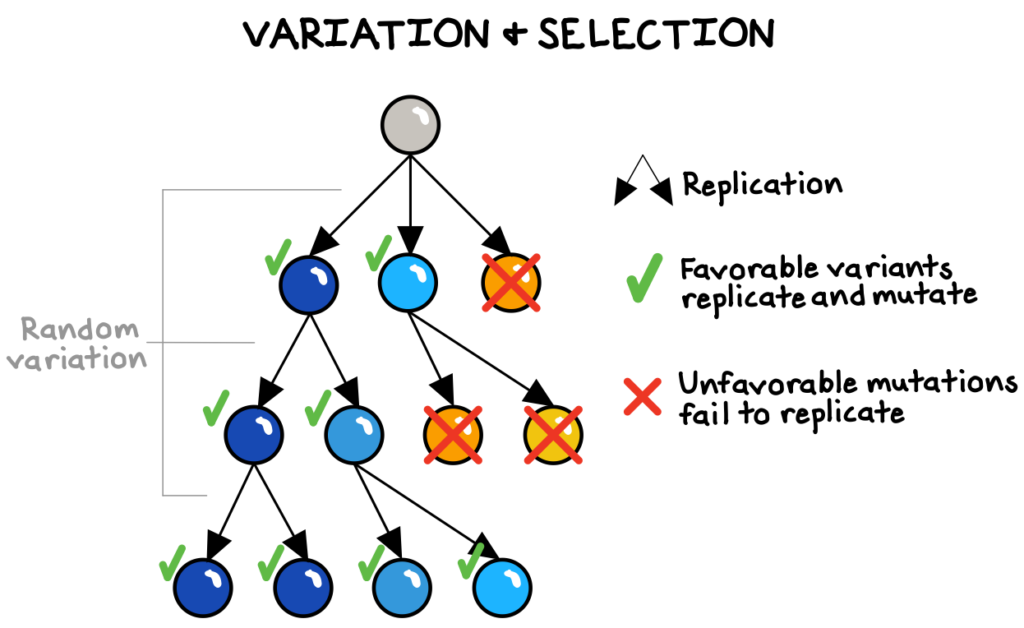
Remarkably, without any intentional “design,” randomness breathes complexity, resilience, and beauty into the world. Driven by evolutionary forces, incredibly complex systems—from human beings to organizational cultures to artificial intelligences—can emerge and function without anyone having consciously designed each of their elements.
In the realm of computer science, programmers have embraced randomness as a problem-solving tool. Randomized algorithms can prove extremely useful when we are stuck. For example, checking random values may help crack complex equations. Many effective “optimization” (or “hill-climbing”) algorithms apply random changes to improve the system whenever it looks like it might be stuck on a local peak. We could “jitter” the system with a few small changes, or we could apply a full “random-restart.”7 Netflix invented a useful resiliency-enhancing tool called “chaos monkey” which deletes random bits of code and shows you how your system reacts.8
***
Embracing randomness can help us to unlock creativity by exploring new ideas and approaches, to eliminate errors of causality, and even to better understand the natural world. We have a choice: we can be astonished or distressed or in denial that the world is unpredictable, or we can admit that we will never have perfect knowledge—and then turn randomness to our advantage.
Notes
- Kahneman, D. (2011). Thinking, Fast and Slow. Farrar, Straus and Giroux. 109-118.
- Gribbin, J. (2004). Deep Simplicity. Random House. 72-74.
- Marletto, C. (2021). The Science of Can and Can’t. Viking. 105-109.
- Stine, R., & Foster, D. (2014). Samples and Surveys. In Statistics for Business: Decision Making and Analysis (2nd ed., pp. 339-354). Pearson Education.
- Ellenberg, J. (2015). How Not to Be Wrong. The Penguin Press. 301-306.
- Deutsch, D. (2011). The Beginning of Infinity. Penguin Books. 89-93.
- Christian, B., & Griffiths, T. (2016). Algorithms to Live By. Henry Holt and Co. 194-197.
- Netflix TechBlog. (2016, October 19). Netflix Chaos Monkey Upgraded [Blog post].