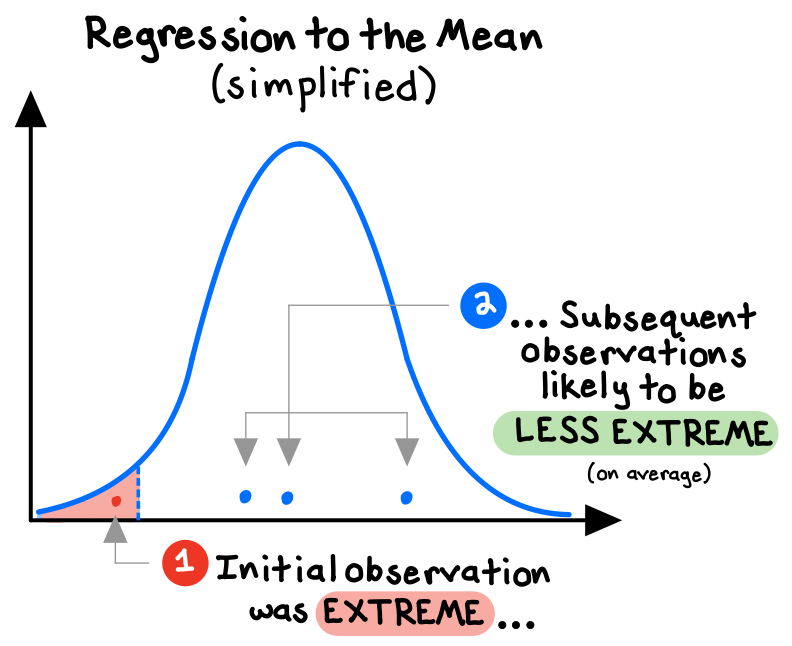
Regression to the mean is the statistical rule that in any complex process that involves some amount of randomness, extreme observations will tend to be followed by more “mediocre” observations.
Although regression to the mean is not a natural law but a statistical tendency, it is an extremely useful mental model, because we have a problematic tendency to get regression wrong. For one, we fail to appreciate its power to explain many apparent phenomena that are really just mirages of randomness. We also often foolishly “predict” regression when what we’ve been observing recently seems extreme.
Innate or random?
It is not some mediocrity-loving law that causes regression to the mean; rather, regression is the natural tendency when inherent characteristics are intermingled with chance. While we should expect inherent traits to show up repeatedly, chance is fleeting.
Consider a clinical trial where we use random sampling to test a new dieting method on overweight folks. Because our body weight fluctuates daily, there is some randomness involved. At initial weigh-ins, the individuals in the heaviest segment are certainly more likely to have a consistent weight problem (an inherent characteristic), but they are also more likely to have been at the top of their weight range on the day you happen to weigh them (a random fluctuation). Therefore, we should expect our heaviest participants to lose some weight on average during the study, regardless of the effectiveness of the diet!1
Causal mirages
The same logic can be applied to outperforming businesses, artistic success, or sports achievement: all of these success cases are more likely to possess superior talent, but also to have had some luck—and luck, by definition, tends to be transitory.
In assessing cause and effect, we commonly attribute causality to a particular policy or treatment when the change in the extreme groups would be expected without the treatment. Regression does not have a causal explanation. It inevitably occurs when the correlation between two elements (such as body weight and a dieting method) is less than perfect—in other words, whenever some amount of randomness is involved.2
In statistical science, the prescription for this causality error lies in introducing a “control group,” which should experience regression effects regardless of treatment. In our dieting study, we would need to compare the results of the dieting group with those of a group who knows nothing of the diet. We then assess whether the outcomes between the control and treatment groups are more different than regression alone can explain.
In everyday life, we must be prudent before assigning causality to some factor when we observe more moderate outcomes following an extreme one. It’s rather tempting to come up with a coherent narrative about what caused a change than to say, “It’s just statistics.” If we believe strings of good or bad results represent a persistent state of affairs, then we will incorrectly label the reversion to normal as the consequence of some other change we made or observed.3
For example, we could come up with stories such as:
- The saleswoman who generated record sales last year but did worse this year must have become less motivated after she got a big bonus.
- The stock market rebound after last year’s recession means the President’s economic policies must be working.
- When I gave my daughter ice cream after she earned an “A+” on a test, she did worse the next time. But when I sternly criticized her after she got a “C,” she did better the next time. Therefore, I should be more forceful.
In all of these examples, it’s possible that the moderation in behavior we observed could be entirely explained by the basic statistical workings of regression to the mean, regardless of the “causal” story we came up with.
An insane example is the purported “discovery” in the 1976 British Medical Journal that bran had an extraordinary balancing effect on digestion. Subjects with a speedy digestion tended to slow down, those with typical digestion speed were unchanged, and those with slow digestion tended to accelerate. The crazy thing is: due to regression to mean, these are exactly the results we should expect to see if the bran had no effect whatsoever!4
***
People tend to prophesy “regression!” after anything extreme happens, without properly understanding why and how it works. Nothing is ever “due” for regression (not the stockmarket, not your football team, etc.). Extreme behavior simply tends not to persist over large samples. Once we understand that the tendency towards mediocrity is inevitable whenever randomness is involved, we can avoid the delusions of causality that plague so many others—whether in business, sports, the stock market, or our weight-loss regimen.