Every time that we attempt to transmit information (a “signal”), there is the potential for error (or “noise”), regardless of whether our communication medium is audio, text, photo, video, or raw data. Every layer of transmission or interpretation—for instance, by a power line, radio tower, smartphone, document, or human—introduces some risk of misinterpretation.
The fundamental challenge we face in communication is sending and receiving as much signal as possible without noise obscuring the message. In other words, we want to maximize the signal-to-noise ratio.
While this concept has been instrumental to the fields of information and communication for decades, it is becoming increasingly relevant for everyday life as the quantity and frequency of information to which we are exposed continues to expand… noisily.
A firehose of noise
Our brains are fine-tuned by evolution to detect patterns in all our experiences. This instinct helps us to construct mental “models” of how the world works and to make decisions even amidst high uncertainty and complexity. But this incredible ability can backfire: we sometimes find patterns in random noise. And noise, in fact, is growing.
By 2025, the amount of data in the world is projected to grow to 175 “zetabytes,” growing by 28% annually.1 To put this in perspective, at the current median US mobile download speed, it would take one person 81 million years to download it all.2
Furthermore, our average number of data interactions are expected to grow from one interaction every 4.8 minutes in 2010, to every 61 seconds in 2020, to every 18 seconds by 2025.3
So, the corpus of data in the world is enormous and growing exponentially faster than the capacity of the human brain. And, the frequency with which we interact with this data is so high that we hardly have a moment to process one new thing before the next distraction arrives. When incoming information grows faster than our ability to process it, the risk that we mistake noise for signal increases, since there is an endless stream of opportunities for us to “discover” relationships that don’t really exist.4
Sometimes, think less
In statistics, our challenge lies in inferring the relevant patterns or underlying relationships in data, without allowing noise to mislead us.
Let’s assume we collected some data on two variables and observed the graphical relationship, which appears to be an upward-facing curve (see charts below). If we tried to fit a linear (single-variable) model to the data, the average error (or noise) between our model’s line and the actual data is too high (left chart). We are “underfitting,” or using too few variables to describe the data. If we then incorporate an additional explanatory variable, we might produce a curved model that does a much better job at representing the true relationship and minimizing noise (middle chart). Next, seeing how successful adding another variable was, we might choose to model even more variables to try to eliminate noise altogether (right chart).
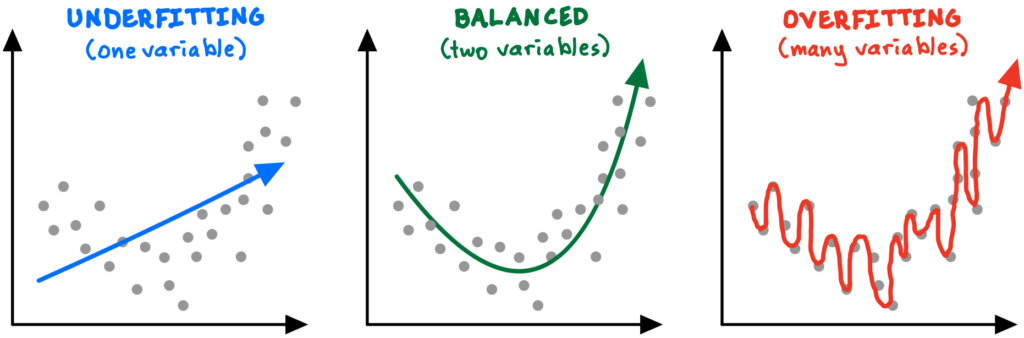
Unfortunately, while adding more factors into a model will always—by definition—make it a closer “fit” with the data we have, this does not guarantee that future predictions will be any more accurate, and they might actually be worse! We call this error “overfitting,” when a model is so precisely adapted to the historical data that it fails to predict future observations reliably.
Overfitting is a critical topic in modeling and algorithm-building. The risk of overfitting exists whenever there is potential noise or error in the data—so, almost always. With imperfect data, we don’t want a perfect fit. We face a tradeoff: overly simplistic models may fail to capture the signal (the underlying pattern), and overly complex algorithms will begin to fit the noise (error) in the data—and thus produce highly erratic solutions.
For scientists and statisticians, several techniques exists to mitigate the risk of overfitting, with fancy names like “cross-validation” and “LASSO.” Technical details aside, all of these techniques emphasize simplicity, by essentially penalizing models that are overly complex. One self-explanatory approach is “early stopping,” in which we simply end the modeling process before it has time to become too complex. Early stopping helps prevent “analysis paralysis,” in which excess complexity slows us down and creates an illusion of validity.5
We can apply this valuable lesson in all kinds of decisions, whether in making business or policy decisions, searching for job candidates, and even looking for a parking spot. We have to balance the benefits of performing additional analyses or searches with the costs of added complexity and time.
“Giving yourself more time to decide about something does not necessarily mean that you’ll make a better decision. But it does guarantee that you’ll end up considering more factors, more hypotheticals, more pros and cons, and thus risk overfitting.”
Brian Christian & Tom Griffiths, Algorithms to Live By (2016, pg. 166)
The more complex and uncertain the decisions we face, the more appropriate it is for us to rely on simpler (but not simplistic) analyses and rationales.
A model of you is better than actual you
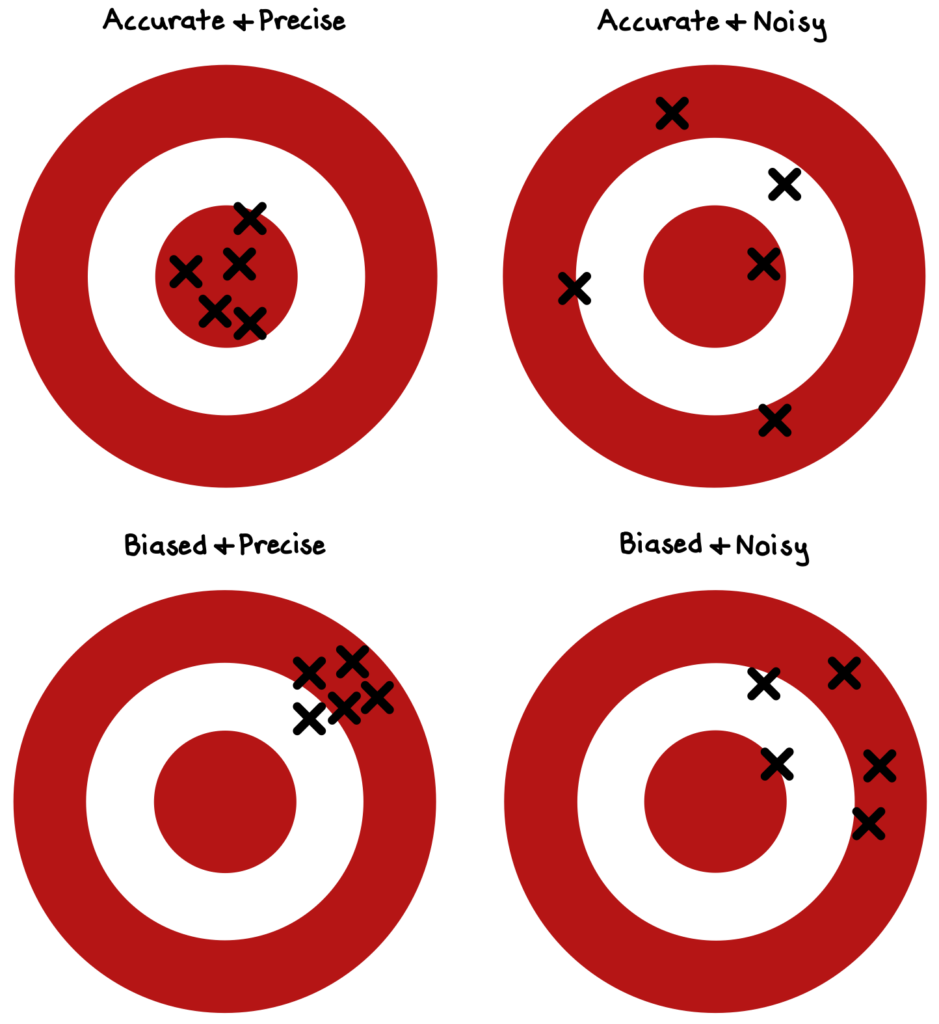
In making professional judgments and predictions, we should seek to achieve twin goals of accuracy (being free of systematic error) and precision (not being too scattered).
A series of provocative psychological studies have suggested that simple, mechanical models frequently outperform human judgment. While we feel more confident in our professional judgments when we apply complex rules or models to individual cases, in practice, our human subtlety often just adds noise (random scatter) or bias (systematic error).
For example, research from the 1960s used the actual case decision records of judges to build “models” of those judges, based on a few simple criteria. When they replaced the judge with the model of the judge, the researchers found that predictions did not lose accuracy; in fact, in most cases, the model out-predicted the professional on which the model was built!
Similarly, a study from 2000 reviewed 135 experiments on clinical evaluations and found that basic mechanical predictions were more accurate than human predictions in nearly half of the studies, whereas humans outperformed mechanical rules in only 6% of the experiments!6
The reason: human judgments are inconsistent and noisy, whereas simple models are not. Sometimes, by subtracting some of the nuance of our human intuitions (which can give us delusions of wisdom), simple models actually reduce noise.
***
In summary, we have a few key takeaways with this model:
- Above all, we should seek to maximize the signal-to-noise ratio in our communications to the greatest practical extent. Speak and write clearly and concisely. Ask yourself if you can synthesize your ideas more crisply, or if you can remove extraneous detail. Don’t let your message get lost in verbosity.
- Second, be aware of the statistical traps of noise:
- Don’t assume that all new information is signal; the amount of data is growing exponentially, but the amount of fundamental truth is not.
- When faced with substantial uncertainty, be comfortable relying on simpler, more intuitive analyses—and even consider imposing early stopping to avoid deceptive complexity.
- Overfitting is a grave statistical sin. Whenever possible, try to emphasize only a few key variables or features so your model retains predictive ability going forward.
- Acknowledge that while human judgment is sometimes imperative, it is fallible in ways that simple models are not: humans are noisy.
References
- Reinsel, D., Gantz, J., & Rydning, J. (2018). Data Age 2025: The Digitization of the World From Edge to Core. IDC, (US44413318).
- Assumes US mobile download speed of 68.34 mbps. Source: Global Median Speeds, Mobile. (2022, September). Speedtest Global Index.
- Reinsel, D., Gantz, J., & Rydning, J. (2018). Data Age 2025: The Digitization of the World From Edge to Core. IDC, (US44413318).
- Silver, N. (2012). The Signal and the Noise. The Penguin Press. 1-18.
- Christian, B., & Griffiths, T. (2016). Algorithms to Live By. Henry Holt and Co. 153-168.
- Kahneman, D., Sibony, O., & Sunstein, C. R. (2021). Noise. Little, Brown Spark. 111-122.